Diện tích mặt cầu là một công thức áp dụng rất nhiều trong suốt năm tháng đi học, cũng như trong thực tiễn. Công thức này sẽ được áp dụng nhiều trong các bài kiểm tra và bài thi tốt nghiệp cấp 3. Chính vì vậy, Giadinhvatreem.vn cùng bạn làm tìm hiểu về vấn đề này!

Các vị trí tương đối của mặt cầu trong không gian
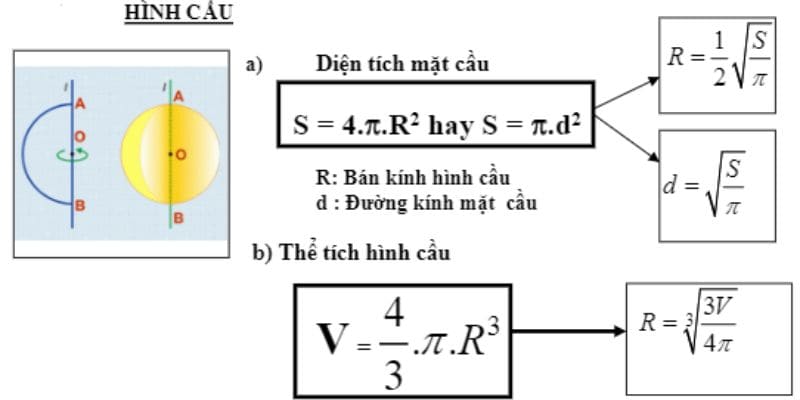
Trong toán học, không gian mặt cầu sẽ tiếp xúc với một số vật thể qua đó người ta ứng dụng sự tiếp xúc này để tính toán, đo đạc chế tạo ra máy móc, động cơ…. Trước khi đi vào các vị trí tương đối, chúng tôi xin giới thiệu đến bạn công thức tính diện tích mặt cầu chuẩn xác nhất:
- Smc = 4*π*R^3 hoặc Smc = π*d^2.
Trong đó:
- Smc: diện tích mặt cầu.
- π: là hằng số pi 3,14.
- R: bán kính mặt cầu.
- d: đường kính mặt cầu.
- Đơn vị diện tích mặt cầu là mét vuông (㎡)….
Vị trí giữa mặt cầu và mặt phẳng trong không gian
Cho mặt cầu S (I;R) và mặt phẳng (Q). Gọi M là hình chiếu vuông góc của I lên (Q) => d = MI là khoảng cách từ điểm I đến mặt phẳng (Q). Khi đó:
- d > R: là mặt cầu và mặt phẳng không có điểm chung.
- d < R: là mặt cầu cắt mặt phẳng theo thiết diện là hình tròn.
- d = R: là mặt cầu tiếp xúc với mặt phẳng: (Q) là mặt phẳng tiếp diện của mặt cầu và M là tiếp điểm.
Lưu ý: Khi mặt phẳng (Q) đi qua tâm I của mặt cầu thì khi đó (Q) được gọi là mặt phẳng kính, và thiết diện được gọi là đường tròn lớn.
Vị trí giữa mặt cầu và đường thẳng trong không gian
Cho mặt cầu S (I;R) và đường thẳng ∆, Gọi M là hình chiếu của I lên ∆ khi đó:
- IM > R: đường thẳng ∆ không cắt mặt cầu.
- IM < R: đường thẳng ∆ cắt mặt cầu tại 2 điểm phân biệt.
- IM = R: đường thẳng ∆ tiếp xúc với mặt cầu, khi đó S là tiếp tuyến, còn M là tiếp điểm.
Mặt cầu nội tiếp, ngoại tiếp hình đa diện trong không gian

- Trong không gian mặt cầu ngoại tiếp hình đa diện, nếu tất cả các đỉnh của hình đa diện đều mặt trên mặt cầu, nói cách khác hình đa diện nội tiếp mặt cầu.
- Mặt cầu ngoại tiếp hình ra diện nếu mặt cầu đó tiếp được tất các mặt của hình đa diện, có thể hiểu rằng hình đa diện ngoại tiếp mặt cầu.
Phía trên là một số định nghĩa, phép bổ trợ để bạn có thể giải các bài toán liên quan đến diện tích mặt cầu. Hãy áp dụng những định lý trên khi gặp bài toán phức tạp, khó nhằn nhé!
Kết luận
Diện tích mặt cầu và các công thức, định nghĩa gắn liền với chúng, đều được chúng tôi cung cấp đến bạn. Hy vọng qua những thông tin trên, bạn đã hiểu rõ hơn về công thức tính diện tích, và vị trí tương đối của mặt cầu. Chúc bạn sẽ đạt điểm cao trong các bài kiểm tra sắp tới!
